이번 시간엔 진동-감쇠 시스템에서 힘 F(t)가 주어졌을때 변위를 전달함수를 이용하여 구해보자.
먼저 시스템의 자유물체도는 다음과 같다.

f(t)는 물체에 가해진 힘이며, 뉴턴의 법칙에 따라 미분방정식은 다음과 같다.
\[m \ddot{x}+b\dot{x}+kx=f(t)\]
\(m=10kg, b=5N\cdot s/m, k=20N/m\)라 하고 초기조건을 \(x(0)=0m, \dot{x}(0)=0m/s\)라 하자.
물리적으로 생각해 보았을 때, f(t)가 일정한 힘을 계속 가한다면 스프링은 늘어나다가 어느 지점에서 힘의 평형을 유지할 것이다.
이제 미분방정식을 Laplace 변환을 해보자. 결과는 다음과 같다.
\[\mathcal{L}\left\{m \ddot{x}+b\dot{x}+kx \right\}=\mathcal{L}\left\{ f(t)\right\}\to ms^2X(s)+bsX(s)+kX(s)=F(s)\]
전달함수는 출력/입력을 나타내는 함수로 여기서 입력은 F(s) 출력은 X(s)이므로 전달함수는 F(s)/X(s) 이다.
따라서 전달함수는 다음과 같다.
\[\frac{X(s)}{F(s)}=\frac{1}{ms^2+bs+k}\]
이제 Simulink를 이용하여 전달함수를 블록선도로 나타내보자. 이번에는 m,b,k를 matlab m-파일로 작성하여 정의해보자.
matlab을 열고, 다음과같이 코드를 작성한다.

m-파일을 저장하고, 코드를 실행시키면 작업공간에 상수가 저장된 것을 알 수 있다.

이제 Simulink를 실행하여 블록을 추가해보자. 전달함수는 라이브러리 - Continuous - Transfer Fcn 블록을 추가하여 얻을 수 있다.

전달함수 블록을 더블클릭하면 분자와 분모를 설정 할 수있다. 작성하는 방법은 가장 높은 차수의 계수부터 행렬로 작성하면 된다. 또한 정의한 상수도 입력이 가능하다. 여기선 분자를 [1], 분모를 [m b k]로 작성한다.

그러면 그림과 같이 num(s)/den(s)로 블록이 생기는데 작성한 전달함수를 나타내고 싶다면 블록을 확대하면 된다.

이제 입력을 무엇을 줄지 생각해보자.
이 모델에서 입력은 힘이므로 1초부터 2N의 힘이 일정하게 가해지도록 step input을 이용해보자.
라이브러리 - Source - Step 블록을 추가하고 전달함수의 입력 포트와 연결하면 다음과 같다.
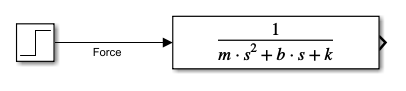
Step 블록을 더블클릭하면 스텝시간, 초기값, 최종값, 샘플시간이 있다.
스텝시간은 입력을 가하는 시간을 말한다.
초기값은 스텝이 일어나기 전에 가해지고 있는 입력을 말한다.
최종값은 스텝을 가할때 입력의 크기를 나타낸다.
여기서는 최종값을 2로 바꾸어보자.

출력을 확인하기 위해 Scope 블록을 추가하면 최종적으로 다음과 같다.

결과를 확인하기전에 중지 시간과 step size를 설정하자. 중지시간은 20초로 설정한다.

step size를 설정하기 위해 모델링 - 모델 설정 - 솔버 에서 솔버 유형을 고정스텝으로 솔버를 ode4로 변경하고, 솔버 세부 정보를 선택하여 고정 스텝 크기를 0.001로 설정한다.

결과를 확인하기 위해 Scope 블록을 더블클릭하여 열고, 실행버튼을 누르면 다음과 같다.
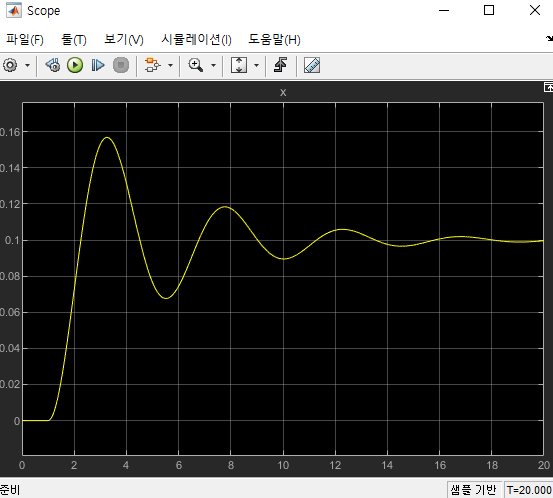
- 1초부터 물체가 진동하기 시작하면서 점점 0.1m에 가까워지는 것을 확인할 수 있다.
결과를 검증하기 위해 전달함수에 최종값 정리를 적용하면 다음과 같다.
\[\displaystyle \lim_{ t\to \infty }x(t)=\displaystyle \lim_{s \to 0}sX(s)=\displaystyle \lim_{s \to 0}s\cdot\frac{1}{ms^2+bs+k}\cdot F(s) =\displaystyle \lim_{ s\to 0}s\cdot\frac{1}{10s^2+5s+20}\cdot \frac{2}{s}=\frac{1}{10}=0.1m\]
'자동제어 > Simulink' 카테고리의 다른 글
| Simulink 기초 (6) 폐루프 제어, Closed loop system : 1.P제어 (0) | 2023.03.26 |
|---|---|
| Simulink 기초 (5) 개루프 제어, open-loop system control (0) | 2023.03.26 |
| Simulink 기초 (3) 2차 시스템 모델링 : 진동-감쇠 시스템, 시뮬레이션 설정 (0) | 2023.03.23 |
| Simulink 기초 (2) 미분방정식 만들기 - 수직하강 문제, 블록 (0) | 2023.03.23 |
| Simulink 기초 (1) 시작하기, 블록 (0) | 2023.03.23 |




댓글