이번엔 2차 미분방정식의 대표적인 형태인 진동-감쇠 시스템을 다뤄보자. 진동 문제의 자유물체도는 다음과 같다.

뉴턴의 법칙에 따라 미분방정식은 다음과 같다.
\[m \ddot{x}+b\dot{x}+kx=0\]
\(m=10kg, b=5kg\cdot m, k=20kg\cdot m^2\)라 하고 초기조건을 \(x(0)=0.1m, \dot{x}(0)=0m/s\)라 하자.
미분방정식의 가장 높은 차수(2차미분)를 왼쪽에 두고 나머지 부분을 오른쪽으로 넘겨보자.
\[m \ddot{x}=-b\dot{x}-kx\]
이는 오른쪽에 있는 두 신호의 합이 왼쪽의 신호가 되는 것을 의미한다.
이제 simulink를 이용하여 시스템을 모델링해보자.
이번에는 m을 gain블록을 이용하여 표현한다(이유는 나중에 나온다), gain 블록은 라이브러리 - Math Operations - gain 블록을 추가하여 얻을 수 있다. gain 블록은 입력 신호를 받아 gain 블록의 계수만큼 곱하여 출력을 한다.
gain 블록을 추가하고 블록을 더블클릭하여 이득을 1/10으로 설정한다. 여기서 이득을 1/10으로 설정하는 이유는 오른쪽의 신호를 받아 합치면 \(10 \ddot{x}\)이 되기 때문이다.

이때 gain 블록의 모양이 -K- 모양이 나오는 경우가 있는는데 블록의 크기를 키우면 해결된다.
gain 블록의 출력 신호는 x2dot을 의미하므로 적분하면 xdot이 나오고 또 적분하면 x가 나올 것이다. 적분기 둘을 추가하고, 신호의 이름을 달아보자.
블록을 추가하는 다른 방법으로는 work space에 블록의 이름을 입력하여 바로 추가할 수 있다. 다음 그림은 이 방법을 이용하여 Integrator 블록을 추가한 예이다.

신호의 이름은 신호를 더블클릭하여 작성할 수 있다.
첫번째 적분기의 출력을 xdot, 두번째 적분기의 출력을 x로 설정해보자.

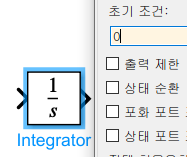

앞에서 설정한 xdot과 x에 대한 초기조건을 적용해보자.
첫번째 적분기에 초기조건 0을 대입하고 두번째 적분기에 초기조건 0.1을 대입한다.
( 왜냐하면 \(\dot{x}(0)=0, x(0)=0.1\)이기 때문이다 )
오른쪽 항의 신호 \(b\dot{x},kx\)를 표현할 때는 앞에서 작성한 xdot 신호와 x 신호에 각각 b와 k를 곱하여 얻을 수 있다.
먼저 xdot 신호와 x신호의 분기점을 생성해보자. Ctrl을 누른 채로 원하는 신호에 마우스를 클릭하여 드래그 하면 분기된 신호를 얻을 수 있다.

gain 블록을 추가하고 나면 입력 포트가 반대쪽에 있어 연결하는데 가시성이 떨어질 수 있다. 그래서 gain 블록 우클릭 후 - 형식 - 블록반전을 누르면 입력포트가 반대쪽으로 정렬된다.

이 외에도 시계방향 회전이나 반시계 방향 회전이 있으니 참고하자.
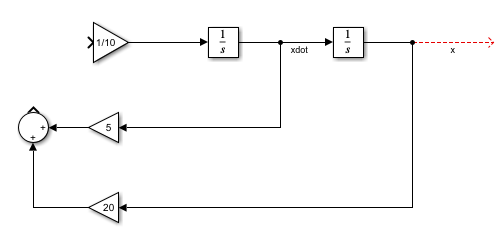
그 다음 xdot 신호와 연결된 gain 블록의 이득은 5, x신호에 연결된 gain 블록의 이득을 20으로 설정하면 다음과 같다.

이제 이 둘의 신호를 합하기 위해 sum 블록을 사용해 볼 것이다. sum 블록은 여러개의 신호를 입력으로 받아 합하거나 빼서 출력 신호를 생성한다.

이 블록은 왼쪽과 아래쪽으로 신호를 받아서 더하고 오른쪽으로 출력하는 의미를 가진다. 이 블록을 더블클릭하면 부호목록이라는 입력 값이 있는데 | 은 \와 shift 를 눌러 쓸수 있고, 포트 공간을 만들때 사용한다.
예를들어 |+|+이면 위에서부터 시계반대방향으로 빈칸 / + / 빈칸 / + 를 의미한다.

+,-는 +는 신호를 더하고 -는 신호를 뺸다는 뜻이다.
먼저 |++로 입력하고 반시계 방향 회전을 이용해서 두 신호를 합해본다. 결과는 다음과 같다.
sum 블록으로 부터 나온 신호의 부호를 바꾸고 1/10을 곱하면 \(\ddot{x}\)을 만들어내는 것을 알 수 있다. 따라서 gain 블록의 이득 값을 -1/10으로 바꿔주고 sum 블록의 출력과 연결한다.
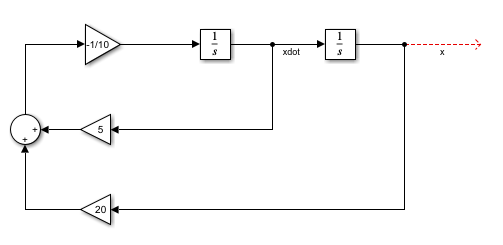
이제 결과를 확인하기 위해 Scope 블록을 추가한다. Scope 블록은 x 신호를 입력으로 받으므로 변위-시간 그래프가 나올 것이다.
* 한편, 이러한 블록선도의 형태는 제어 가능 표준형(Controllable Canonical Form)이라 한다. 제어 가능 표준형에 대해 공부하면 임의의 전달함수를 가진 시스템을 모델링하는데 도움이 될 것이다. 이 부분은 제어공학에서 따로 다루도록 하겠다.

결과를 확인하기 전에 간단하게 시뮬레이션을 설정해보자. 10초동안의 응답을 보기 위해 시뮬레이션 탭에 중지시간을 10으로 변경한다.

Simulink에서 미분방정식을 풀때는 수치해석 방법을 이용하여 해를 구한다. 따라서 수치해석 방법과 step size를 설정해야 할 필요가 있다.
먼저 모델링 탭 - 모델설정 을 들어가면 시뮬레이션 시간과 솔버선택이 있다. 솔버 선택에서 가변스텝을 고정스텝으로 변경하고, ode4(Rounge Kutta method)를 선택한다(Rounge Kutta method가 가장 많이 쓰이는 수치해석 방법이다)
그리고 솔버 세부 정보를 클릭하면 고정스템크기를 찾을 수 있는데 이를 0.0001초로 변경한다.

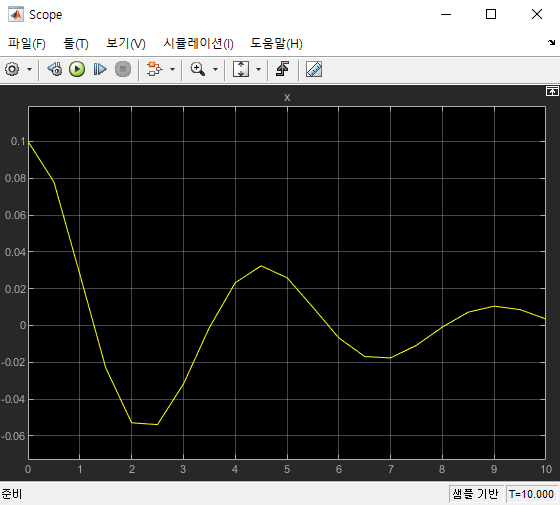
이제 Scope를 열고 실행 버튼을 누르면 결과가 출력된다.

진동 감쇠 시스템의 응답이 잘 표현된 것을 알 수 있다. 여기서 step size를 늘려보자.
모델- 모델 설정-고정 스템 사이즈를 0.5로 설정한다.
그러면 이렇게 그래프가 부드럽지 않은 것을 알 수 있고 Error가 생길 수도 있다. 따라서 step size는 상황에 맞게 잘 설정해야한다.
'자동제어 > Simulink' 카테고리의 다른 글
| Simulink 기초 (6) 폐루프 제어, Closed loop system : 1.P제어 (0) | 2023.03.26 |
|---|---|
| Simulink 기초 (5) 개루프 제어, open-loop system control (0) | 2023.03.26 |
| Simulink 기초 (4) 전달함수, 블록선도 : 진동 - 감쇠 시스템 (0) | 2023.03.24 |
| Simulink 기초 (2) 미분방정식 만들기 - 수직하강 문제, 블록 (0) | 2023.03.23 |
| Simulink 기초 (1) 시작하기, 블록 (0) | 2023.03.23 |




댓글